Departmental PhD Thesis Exams
Past PhD Defenses
Wenyi (Reila) Zheng
September 12th, 2025
10:00 a.m. (sharp)
BA6180, 40 St George St. / Zoom Web Conference
PhD Candidate: Wenyi(Reila) Zheng
Supervisor: Giulio Tiozzo
Thesis title: Combinatorial Structure of Parameter Spaces of Polynomials
Copy of Wenyi (Reila) Zheng's Thesis
In this thesis, we will explore the combinatorics of the Mandelbrot set. Firstly, I will discuss relates the ordering of the hyperbolic components along veins to a classical result of Sharkovsky of orbit forcing for maps of one real dimension. In this problem I will assume V is a principal vein of combinatorial rotation number p/k (and denote i = 1), or an i-th secondary vein for 2 ≤ i ≤ k − 1. Suppose CV (n) is the hyperbolic component of period n along V closest to the main cardioid. I will show that CV (n) ≻V CV (m) if n >k m. Additionally, the hyperbolic components of CV (n) with n ≡ i mod k are minimal and form a dynamically simple family whose Hubbard trees are spiral graphs. Secondly, I will discuss a characterization of a family of abstract Hubbard trees by their topology. For any n ≥ 3, let M(n) denote the set of parameters c in the Mandelbrot set with Hubbard tree Tc homeomorphic to an n-star. An n-vein is a union of veins in the Mandelbrot set that is homeomorphic to an n-star. I will show that the set of parameters of M(n) is a exactly the union of ϕ(n) n-stars and the hyperbolic components that pass through them. Additionally, I will identify a family of dynamically simple Misiurewicz tips that define the n-veins. Thirdly, I will extend Milnor-Thurston kneading theory to the dynamics of Hubbard trees of postcritically finite maps. Using the first return map of a suitable interval, I will give an algorithm to find the kneading determinant for the Hubbard trees of along an arbitrary vein to a Misiurewicz tip, by identifying the kneading determinant of the tip and perturbing it for on the portion that shares the same branching. Lastly, I will give another description of the contributions to pseudomonodromy of the Mandelbrot set. Given an oriented arc in the exterior of the Mandelbrot set that starts and ends at the root of the same hyperbolic component, it induces an automorphism on the space of kneading sequences. Ishii-Richards showed that the nontrivial contributions of this automorphism of kneading sequences arise from conspicuous components. I will present a natural description of conspicuous components using internal addresses.
Oleksandr (Alik) Sokolov
September 11th, 2025
10:00 a.m. (sharp)
BA6290B, 40 St George St. / Zoom Web Conference
PhD Candidate: Oleksandr (Alik) Sokolov
Supervisor: Luis Seco
Thesis title: From Theory to Practice a Stochastic Framework for Utility Driven Capital Allocation_compressed
Copy of Oleksandr Sokolov's Thesis_compressed
In this thesis, we study utility-driven capital allocation on causal graphs that encode real economic drivers, with a particular focus on multi-period stochastic control and externalities. The central question is to what extent a semantically grounded causal feature map, together with an externality-aware utility function, can be used to model the economically meaningful policies, allocations, and structural interventions between states of the economy.
More precisely, motivated by dynamic programming, production-based asset pricing, and integrated climate-economic models, we formulate a multi-period optimization problem over resource, capacity, and policy controls on a directed acyclic causal graph. This formulation propagates policy interventions along structural edges and keeps both forecasts and allocations interpretable. We make progress on three fronts.
In terms of robustness, we prove that bounded forecast error perturbs the multi-period value by at most O(ε) under Lipschitz and compactness assumptions. In a computational direction, we show that deciding whether any finite horizon policy attains a target discounted utility is NP-complete via a reduction from 0–1 Knapsack. In a representation-theoretic direction, we establish conditions under which learned low-dimensional dynamics are strict contractions, implying a unique fixed point and geometric convergence of iterative algorithms in latent spaces. Altogether, the thesis shows how causal graphs combined with externality-aware utility functions can help determine optimal allocations and interventions in an interpretable fashion, and provides mathematical guarantees that make such models tractable for long-horizon decision making.
Kirill Kashkan
September 9, 2025
10:00 a.m. (sharp)
BA6180, 40 St George St. / Zoom Web Conference
PhD Candidate: Kirill Kashkan
Supervisor: Almut Burchard
Thesis title: Dense Forests with Low Visibility
Copy of Kirill Kashkan's Thesis
A dense forest in Rd is a set of points with finite density such that any line segment of length V(ε), the visibility function of the forest, comes within distance ε of an element of the set—the points with a ball of radius ε centred at them can be viewed as trees obstructing visibility, hence the name. Such sets are known to exist. The problem now is to determine how small the visibility can be made and how many additional properties can be required from a dense forest. This thesis presents results in those directions. In this thesis, a dense forest is constructed by modifying a base set obtained from a Poisson point process by adding some points to it such that the visibility is in O ( ε−(d−1) ln ε−1). Further, the Poisson point process can be adjusted so that the base set is uniformly discrete while maintaining the same final visibility. Due to the latter addition of points, the resulting dense forest is not uniformly discrete Through a slight change of perspective—from eliminating lines of sight to eliminating empty regions—the problem of finding dense forests is closely related to Danzer’s problem. It asks if there exists a set of finite density intersecting every convex set of volume 1. A relaxation of Danzer’s problem is examined where the volume of the convex sets is allowed to grow as their eccentricity increases. Bounds on the growth of the volume are obtained by adapting the approach taken for dense forests earlier.
Matthew Koster
September 5th, 2025
10:00 a.m. (sharp)
BA6180, 40 St George St. / Zoom Web Conference
PhD Candidate: Matthew Koster
Supervisor: Eckhard Meinrenken
Thesis title: Flat symplectic bundles over a Riemann surface
Copy of Matthew Koster's Thesis
We study flat projective symplectic bundles over closed Riemann surfaces. A Milnor-Wood type inequality is established using the Maslov index to classify the isomorphism classes of principal PSp(2n;R)-bundles admitting a flat connection. Special attention is given to the case n = 1 corresponding to PSL2(R) where explicit topological descriptions of commutator fibers are obtained, revealing their structure as 3-manifolds. This thesis also explores the interpretation of flat PSL2(R)-bundles in terms of singular hyperbolic geometry via holonomy representations, providing an explicit correspondence between flat connections and hyperbolic structures (with singularities). These geometric techniques are applied to analyze the maximal components of the moduli space where Teichmüller space is a distinguished connected component corresponding to maximal representations.
Caleb Jonker
September 3, 2025
10:00 a.m. (sharp)
BA6290, 40 St George St. / Zoom Web Conference
PhD Candidate: Caleb Jonker
Supervisor: Marco Gualtieri
Thesis title: Curvatures in generalized Kähler geometry
Bi-Hermitian is an extension of Kähler geometry which arose first in the study of supersymmetric σ-models in the 1980s. It was later rediscovered by Gualtieri, within Hitchin’s generalized geometry program, and rechristened as generalized Kähler geometry. In this thesis, we study a wide variety of curvatures that appear in generalized Kähler geometry. Using the structure provided by the generalized Kähler geometry we identify Chern connections on the canonical bundles of the generalized complex structures and relate these to the Bismut connections of the underlying bi-Hermitian manifold. We then identify these connections as components of generalized Chern connections and, as a result, obtain symmetries of the generalized complex structures which may be described in terms of bi-Hermitian data. We identify a second type of generalized Chern connection arising from the holomorphic Poisson structures present on any generalized Kähler manifold. Using a description of these involving bi-Hermitian data, we give a novel reformulation of generalized Kähler-Ricci flow in terms of purely generalized geometric data.
The main tool that we use to accomplish this is the Roytenberg algebra, which is the algebra of functions on the graded symplectic manifold corresponding to the underlying Courant algebroid. We describe the structure inherited by the Roytenberg algebra in the presence of a generalized Kähler structure and gives a characterization of the integrability condition in terms of the Roytenberg algebra.
Ethan Ross
August 27, 2025
2:00 p.m. (sharp)
BA6183, 40 St George St. / Zoom Web Conference
PhD Candidate: Ethan Ross
Supervisor: Lisa Jeffrey
Thesis title: Stratified Vector Bundles and Geometric Quantization
Geometric Quantization is a family of procedures which take as input a decorated symplectic manifold and produces a complex vector space. This thesis develops an extension of this framework to a class of singular spaces called stratified symplectic spaces. This approach necessitated the development of the theory of stratified vector bundles and distributions. As an application, I showed that quantization commutes with reduction for singular quotients of toric manifolds and cotangent bundles.
Ramon Ronzon Lavie
August 26, 2025
2:00 p.m. (sharp)
BA6183, 40 St George St. / Zoom Web Conference
PhD Candidate: Ramon Ronzon Lavie
Supervisor: Edward Bierstone
Thesis title: Partial Desingularization Preserving Normal Crossings and Minimal Singularities in Low Dimension
Copy of Ramon Ronzon Lavie's thesis
In this work, we address the problem of partial desingularization while preserving normal crossings for algebraic varieties of dimension ≤ 4 defined over an algebraically closed field of characteristic zero. The main result provides a sequence of smooth blowings-up where each blow-up preserves the normal crossings locus and such that the resulting variety has only singularities in a given minimal finite list N, where each element in N is expressed in a precise local normal form. These elements are described using determinants of circulant matrices, which are the n×n matrices spanned by the permutation matrices associated to cyclic permutations of Sn. This result is the best possible since, in general, there is no resolution procedure which preserves the normal crossings locus and such that the resulting variety has only normal crossings singularities.
Emily Erlebach
Thursday, August 21, 2025
10:00 a.m. (sharp)
BA6183, 40 St George St. / Zoom Web Conference
PhD Candidate: Emily Erlebach
Supervisor: Stevo Todorcevic
Thesis title: Proper Forcing, The P-Ideal Dichotomy, and the S-space Problem
Copy of Emily Erlebach's Thesis
In this thesis, we will explore the relationship between the S-space problem and the Proper Forcing Axiom (PFA). In particular, we will show that many consequences of PFA are compatible with the existence of various S-spaces.
We will start by studying the notion of solid graph, first introduced by Soukup, and show this can be used to encode many objects whose existence follows from ♢ or CH. We will show that Neeman iterations preserve solid graphs, providing a general tool for preserving such objects while forcing consequences of PFA.
Next, we will then introduce two new types of graph, namely (m, n)-solid graphs and HF graphs. These new notions can encode many different S-spaces, including strong HFD spaces, strong HFDw spaces, and first countable strong O-spaces. We will show that much of the theory of solid graphs extends to these new notions, including the preservation by Neeman iterations.
From here, we will be able to construct models with many consequences of PFA plus the aforementioned S-spaces. Using (m, n)-solid graphs, we will construct models with p = ℵ2, the Mapping Reflection Principle, the Open Graph Axiom, Baumgartner’s Axiom, and all Aronszajn trees are club isomorphic. Using HF graphs, we will construct models with s = ℵ1, add(M) = ℵ2, the Mapping Reflection Principle, and the P-Ideal Dichotomy. Most notably, this provides a partial negative answer to a question of Todorˇcevi´c about whether the P-Ideal Dichotomy and b > ℵ1 implies there are no S-spaces.
Ivan Salgado
Tuesday, 19 August, 2025
2:00 p.m. (sharp)
BA6183, 40 St George St. / Zoom Web Conference
PhD Candidate:Ivan Salgado
Supervisor: Robert Jerrard
Thesis title: Approximate Solutions to the Superconducting Interface Model
We examine various aspects of the Superconducting Interface Model
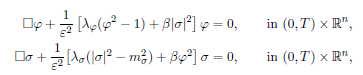
For 0 < ε ≪ 1, for certain choices of positive parameters (λφ, λσ, mσ, β), and with (φ, σ) taking values in R × C. This model was introduced by Kyle Thompson in [34], who considers equivariant solutions with n = 2 and proves, modulo a spectral assumption, the existence of solutions such that φ ≈ +1 or φ ≈ −1 except in a transition layer of thickness O(ε) around a hypersurface Γ, while σ is exponentially small except near Γ. In this context, σ is interpreted as carrying a superconducting current confined to the transition layer around Γ. Moreover, as a result of the equivariant assumption, Γ is required to be a surface traced by a circle whose radius varies in time. A main contribution of [34] is to derive the laws of motion, in the form of an ODE, according to which the geometry of Γ changes due to the flow of current within Γ, in the limit ε → 0.
In this thesis, we extend these results in several ways. First, we carry out a careful analysis of the static 1-dimensional superconducting interface model, including a proof of the spectral condition assumed in [34] for a range of
the model parameters. This completes the rigorous derivation of the laws of motion in the 2-dimensional equivariant case. Additionally, in arbitrary dimensions and without any symmetry assumptions, we provide a rigorous
construction of approximate solutions of arbitrary order for the superconducting interface model, yielding a formal derivation of the laws of motion for a superconducting interface in full generality. Finally, we prove the well-posedness
for smooth data of these laws of motion for a suitable choice of gauge.
Leo Jiang
Wednesday, July 16, 2025
10:00 a.m. (sharp)
BA6183, 40 St George St. / Zoom Web Conference
PhD Candidate: Leo Jiang
Supervisor: Joel Kamnitzer
Thesis title: Topology of real matroid Schubert varieties
In this thesis, we study the topology of real matroid Schubert varieties, which are closures of real linear spaces in products of projective lines. We show that the topology of these varieties is controlled by the combinatorics of real hyperplane arrangements. More precisely, we exhibit homeomorphisms from real matroid Schubert varieties to quotients of zonotopes. Further, this combinatorial model for the topology of the variety can be generalised to define a topological space for any oriented matroid. As a consequence, we are able to compute the fundamental group and integral cohomology of these spaces, obtaining virtual Coxeter groups (in special cases) and signed analogues of the graded Möbius algebra, respectively.
Chengjin (Jessica) Liu
Wednesday, July 9, 2025
2:00 p.m. (sharp)
BA6183, 40 St George St. / Zoom Web Conference
PhD Candidate: Chengjin (Jessica) Liu
Supervisor: Dror Bar-Natan
Thesis title: A Proof of the Kashaev Signature Conjecture
The Levine-Tristram signature is a well-known invariant of links that is topological in nature – its known definitions rely on manifolds associated with the link and it is related to other topological invariants such as genus, unlinking number, and the Alexander polynomial. In 2018 Kashaev introduced a link invariant defined using a simple algorithm on link diagrams which he conjectured also computes the Levine-Tristram signature [Kas21]. In this thesis we present a method of obtaining Kashaev’s invariant using the original Seifert surface definition of the Levine-Tristram signature, making evident the relationship between the two and thereby proving Kashaev’s conjecture. We obtain as a corollary another formula for the Alexander polynomial. The content of this thesis is based on [Liu25].
Shuofeng (Simon) Xu
Tuesday, June 24th, 2025
2:00 p.m. (sharp)
63 St. George Street, Room 111/ Zoom Web Conference
PhD Candidate: Shuofeng (Simon) Xu
Supervisor: Daniel Litt
Thesis title: On topological and Hodge theoretic invariants of curves and families of curves
Copy of Shuofeng (Simon) Xu's Thesis
In this thesis, we study topological and Hodge theoretic invariants associated to smooth complex algebraic varieties with particular focuses on algebraic curves and smooth projective families of curves. The central question we would like to understand is to what extent these invariants capture morphisms between the corresponding varieties.
More precisely, inspired by Grothendieck’s section conjecture in anabelian geometry, we formulated and studied a topological and a Hodge theoretic section question for smooth projective family of curves and made progress towards answering those questions. In the topological setting, many of our results are analogous to existing results in anabelian geometry. In the Hodge setting, much less is known, and so we also studied the connection between the Hodge theoretic section question and classical results in nonabelian
Hodge theory. In a different direction, motivated by the famous theorem of Torelli, we studied if the Torelli’s theorem can be made functorial. We construct interesting examples of morphisms of Hodge structures which do not arise from morphism between curves, and connect our construction to the study of isotrivial isogeny factors in family of curves.
Evan Sundbo
Wednesday, June 4, 2025
10:00 a.m. (sharp)
BA6183/ Zoom Web Conference
PhD Candidate: Evan Sundbo
Supervisor: Michael Groechenig
Thesis title: Broken Toric Varieties and Hypertoric Hitchin Systems
In the first part of this thesis we study the cohomology of broken toric varieties via the derived push-forward of the constant sheaf to a complex of polytopes, thus proving a Deligne-type decomposition theorem, degeneration of the associated Leray-Serre spectral sequence, and showing that the Leray filtration on their cohomology is equal to the weight filtration (up to re-indexing). We discuss certain maps between broken toric varieties and how they descend to maps of cohomology groups. Furthermore, we give a description of the Betti numbers of some broken toric varieties whose associated complex of polytopes is then skeleton of a higher dimensional polytope, encompassing some important examples. In the second part we investigate hypertoric Hitchin systems, whose cohomology is governed by a subvariety which is broken toric. After reviewing their construction, we give a new proof of a deletion-contraction relationship on these varieties (first proven by Dansco-McBreen-Shende) and refine it to a statement about the cohomology of certain sheaves on the polytope complex. Using these facts and the general results in the first chapter, we develop tools for calculating the cohomology of some families of hypertoric Hitchin systems inductively, given knowledge of a base case. In particular, this yields explicit formulae for the Betti numbers of hypertoric Hitchin systems associated to graphs with first Betti number 2.
Bruno Staffa
Friday, May 23, 2025
10:00 a.m. (sharp)
BA6183/ Zoom Web Conference
PhD Candidate: Bruno Staffa
Supervisor: Yevgeny Liokumovich
Thesis title: On density and equidistribution of stationary geodesic nets
See poster for abstract.
Xincheng Zhang
Tuesday, May 5th, 2025
10:00 a.m. (sharp)
BA6183/ Zoom Web Conference
PhD Candidate: Xincheng Zhang
Supervisor: Jeremy Quastel
Thesis title: TASEP and the KPZ Fixed Point in Half-Space-Xincheng Zhang
In this thesis, we present the multi-point probability distribution of the totally asymmetric exclusion process (TASEP) in the half-space, starting from a general deterministic initial condition. More precisely, let h(t,x) denote the height function of the TASEP at position x and time t. We provide an explicit formula for P(h(t,x1) ≤ r1, . . . ,h(t,xm) ≤ rm). This formula is well-suited for scaling limit analysis. By applying a 1:2:3 scaling, we derive the probability distribution for the half-space KPZ fixed point, which is conjectured to represent the universal process for KPZ universality models restricted to a half-space. Additionally, we introduce a new formula for the full-space TASEP, starting from a general initial condition. This formula differs from the one derived by Matetski et al.
Feodor Kogan
Tuesday, April 29th, 2025
10:00 a.m. (sharp)
BA6183/ Zoom Web Conference
PhD Candidate: Feodor Kogan
Supervisor: George Elliott
Thesis title: Groupoid Models of Irrational Rotation Algebras
It is known that every classifiable C∗-algebra has at least countably many non-isomorphic groupoid models. We explore this phenomena for irrational rotations algebras by restricting the Kronecker flow on the torus to various transversals and analyzing what happens to the dynamics under the action of SL2(Z). By "decoupling" bouquets of circles within the torus we produce new groupoids and then proceed to study their invariant measures and equivalences. This allows us to produce groupoid models of irrational rotation algebras, whose object spaces are arbitrary finite disjoint unions of circles. These constructions allows us to see projections in the algebra in a geometric fashion and provide an example of how Rieffel-Morita equivalence of C∗-algebras can be produced from equivalence of groupoids.
Kyle Waller Bower
Monday, February 10, 2025
10:00 a.m. (sharp)
63 St. George Street, Room 111/ Zoom Web Conference
PhD Candidate: Kyle Waller Bower
Supervisor: Adam R. Stinchcombe and Spyros Alexakis
Thesis title: The Electrostatic Problem for Piecewise Constant Conductivities in Two Dimensions: Numerical Methods and Optimal Regularity
We present a numerical method for solving the elliptic partial differential equation problem for the electrostatic potential with piecewise constant conductivity and a Neumann boundary condition. Our method employs an integral equation approach for which we derive a system of well-conditioned integral equations by representing the solution as a sum of single-layer potentials. The fast multipole method is used to accelerate the generalized minimal residual method solution of the integral equations. For efficiency, we adapt the grid of the Nyström method based on the spectral resolution of the layer charge density. Additionally, we present a method for evaluating the solution, based on up-sampling and the boundary element method, that is efficient and accurate throughout the domain, circumventing the close evaluation problem. To support the design choices of the numerical method, we derive regularity estimates with bounds explicitly in terms of the conductivities and the geometries of the boundaries between their regions. The resulting method is fast and accurate for solving the electrostatic potential in media with piecewise constant conductivities. We also provide analytical results for the system of equations for the charge densities. Firstly, we establish the existence and uniqueness of this system of equations. Secondly, we derive regularity for the charge densities along each interface. We show that assuming that the interface has C k regularity, then the charge density is of regularity H k (i.e., in the Hilbert space of order k). Furthermore, we generalize our results by considering the case where the piecewise constant regions of conductivity overlap and we study the behavior of the solution to leading order at points of intersection between two transversely intersecting interfaces of regions of piecewise constant conductivity.
Ahmed Ellithy
Wednesday, December 11, 2024
1:30 p.m. (sharp)
BA6183/ Zoom Web Conference
PhD Candidate: Ahmed Ellithy
Supervisor: Spyros Alexakis
Thesis title: Existence of Static Vacuum Extensions for Near-Schwarzschild Spheres
We establish the local well-posedness of the Bartnik static metric extension problem for arbitrary Bartnik data that perturb that of any sphere in a Schwarzschild {t = 0} slice. Our result in particular includes spheres with arbitrary small mean curvature. We introduce a new framework to this extension problem by formulating the governing equations in a geodesic gauge, which reduce to a coupled system of elliptic and transport equations. Since standard function spaces for elliptic PDEs are unsuitable for transport equations, we use certain spaces of Bochner-measurable functions traditionally used to study evolution equations. In the process, we establish existence and uniqueness results for elliptic boundary value problems in such spaces in which the elliptic equations are treated as evolutionary equations, and solvability is demonstrated using rigorous energy estimates. The precise nature of the expected difficulty of solving the Bartnik extension problem when the mean curvature is very small is identified and suitably treated in our analysis.
Max Klambauer
Monday, September 30, 2024
1:00 p.m. (sharp)
BA6183/ Zoom Web Conference
PhD Candidate: Max Klambauer
Supervisor: Steve Kudla
Thesis title: Symplectic Theta Functions and Theta Lifts of Modular Forms to Split Orthogonal Groups
See poster for abstract.
Jinhui Li
Thursday, September 12, 2024
2:00 p.m. (sharp)
BA6183/ Zoom Web Conference
PhD Candidate: Jinhui Li
Supervisor: Luis Seco
Thesis title: Advanced Optimization Techniques in Dynamic Portfolio Strategies, Pair Trading, and Carbon Dioxide Emission Modeling
AI technologies are revolutionizing the world at a very fast pace. I believe that in the future, they can revolutionize math research as well. In this thesis, we developed novel portfolio construction models that integrate Bayesian Markov Switching Models with clustering algorithms, designed to optimize dynamic portfolio strategies. Additionally, we introduced a Multi-modal Temporal Relation Graph Learning framework to discern pair trading patterns, and an optimization framework incorporating Support Vector Machine regression and Principal Component Regression to refine carbon dioxide emission forecasting.
Detailed convergence analyses were conducted for both the Bayesian Markov Switching Model and the MTRGL framework, ensuring that these models efficiently reach stable solutions. These methodologies have demonstrated superior risk-adjusted returns, improved trading pattern recognition, and enhanced accuracy in emission modeling, showcasing the transformative potential of AI-driven optimization and mathematical models in quantitative finance and sustainability.
Matthew Sunohara
Wednesday, September 11, 2024
1:30 p.m. (sharp)
BA6183/ Zoom Web Conference
PhD Candidate: Matthew Sunohara
Supervisor: Jim Arthur
Thesis title: On Stable Harmonic Analysis and Stable Transfer
See poster for abstract.
Virginia Pedreira
Tuesday, September 10, 2024
10:00 a.m. (sharp)
Zoom Web Conference
PhD Candidate: Virginia Pedreira
Supervisor: Bálint Virág
Thesis title: Ordering of the Tracy-Widom beta distributions and fractal dimension of the level sets of the directed landscape
See poster for abstract.
Lemonte Alie-Lamarche
Tuesday, September 10, 2024
1:00 p.m. (sharp)
BA6183/ Zoom Web Conference
PhD Candidate: Lemonte Alie-Lamarche
Supervisor: Bálint Virág
Thesis title: The Hausdorff Dimension of the Level Sets of the Directed Landscape
See poster for abstract.
Leonard Afeke
Friday, August 30, 2024
10:00 a.m. (sharp)
BA6183/ Zoom Web Conference
PhD Candidate: Leonard Afeke
Supervisor: Dror Bar-Natan
Thesis title: On the Gassner invariant of braids and string links
See poster for abstract.
Keyou Zeng
Thursday, August 29, 2024
11:00 a.m. (sharp)
Zoom Web Conference
PhD Candidate: Keyou Zeng
Supervisor: Kevin Costello & Nick Rozenblyum
Thesis title: Holography and Koszul Duality in Quantum Field Theory.
See poster for abstract.
Dong Hao Ou Yang
Wednesday, August 28, 2024
2:00 p.m. (sharp)
BA6183/ Zoom Web Conference
PhD Candidate: Dong Hao Ou Yang
Supervisor: Michael Sigal
Thesis title: Approach to Equilibrium in Markovian Open Quantum Systems
Open quantum systems arise from quantum systems interacting with quantum environments after the latter’s degrees of freedom are “integrated" out. No extra assumptions, besides the standard self-adjointness assumptions, are required. This class of systems is the bedrock of quantum non-equilibrium statistical mechanics and quantum information theory. The dynamics of such systems are usually studied under an additional assumption that they are Markovian. In that case, they are governed by the von Neumann-Lindblad equation.
In this thesis, we study the evolution of Markovian open quantum systems. We show that, under certain conditions (including quantum detailed balance condition), the evolution converges to the space of stationary states, which, under additional assumptions, is spanned by a single – equilibrium – state. The latter property is known as the return to equilibrium. Our approach could be treated as spectral analysis on non-commutative spaces.
Daniel Hudson
Wednesday, August 28, 2024
11:00 a.m. (sharp)
BA6183/ Zoom Web Conference
PhD Candidate: Daniel Hudson
Supervisor: Eckhard Meinrenken
Thesis title: Groupoids in the Category of Weighted Manifolds
See poster for abstract.
Tianyu Zhou
Monday, August 26, 2024
2:00 p.m. (sharp)
BA6183/ Zoom Web Conference
PhD Candidate: Tianyu Zhou
Supervisor: Catherine Sulem
Thesis title: Nonlinear modulation of surface water waves over a periodic bottom
This thesis contributes to the study of the two-dimensional water wave problem in the presence of a variable bottom topography, which describes the motion of a free surface over a body of water under the influence of gravity. When the bottom topography is flat (with depth possibly infinite), it is known that, in a weakly nonlinear regime, the envelope of modulated surface waves is governed by the cubic nonlinear Schrodinger (NLS) equation. This result was derived in the case of infinity depth by Zakharov (1986), and later extended to finite depth domains over a flat bottom by Hasimoto and Ono (1978).
In this thesis, we extend this derivation to the two-dimensional water wave problem in the case of a variable bottom, assumed to be a smooth periodic function. Starting from the Zakharov/Craig-Sulem formulation of water waves, we use a multiple-scale method to write the surface wave in the form of a slowly modulated Bloch-Floquet wavepacket, which propagates at the group velocity. We show that the envelope of wave amplitude is governed by the NLS equation. A key step in this process is to investigate the actions of the Dirichlet-Neumann operator on multiple-scale functions of various forms. We also present perturbative calculations of the Bloch-Floquet eigenvalues and eigenfunctions of the Dirichlet-Neumann operator when the variation of periodic bottom is small. These are used to study the effect of the variable bottom on the coefficients in the NLS equation.
Mariam Alhawaj
Thursday, August 22, 2024
9:00 a.m. (sharp)
BA6183/ Zoom Web Conference
PhD Candidate: Mariam Alhawaj
Supervisor: Giulio Tiozzo
Thesis title: Generalized pseudo-Anosov maps arising from holomorphic dynamics
In this thesis, we develop a new connection between the dynamics of quadratic polynomials on the complex plane and the dynamics of homeomorphisms of surfaces. In particular, given a quadratic polynomial, we investigate whether one can construct an extension of it which is a generalized pseudo-Anosov homeomorphism. Generalized pseudo-Anosov means it preserves a pair of foliations with infinitely many singularities that accumulate on finitely many points. We determine for which quadratic polynomials such an extension exists. The construction is related to the dynamics on the Hubbard tree, which is a forward invariant subset of the filled Julia set containing the critical orbit. We define a type of Hubbard trees, which we call crossing-free, and show that these are precisely the Hubbard trees for which one can construct a generalized pseudo-Anosov map.
Sebastian Gherghe
Monday, August 12, 2024
2:00 p.m. (sharp)
BA6183/ Zoom Web Conference
PhD Candidate: Sebastian Gherghe
Supervisor: Michael Sigal
Thesis title: On Quantum Adiabatic Dynamics
See poster for abstract.
Soheil Memariansorkhabi
Monday, July 29, 2024
2:00 p.m. (sharp)
BA1230/ Zoom Web Conference
PhD Candidate: Soheil Memariansorkhabi
Supervisor: Jacob Tsimerman
Thesis title: Hyperbolicity and Rational Points on Complex Ball Quotients
See poster for abstract.
Dinushi Munasinghe
Tuesday, July 16, 2024
11:00 a.m. (sharp)
BA6183/ Zoom Web Conference
PhD Candidate: Dinushi Munasinghe
Supervisor: Dror Bar-Natan, Ben Webster
Thesis title: Schur Algebras in Type B
We compare two type B generalizations of the $q$-Schur algebra: the cyclotomic $q$-Schur algebra of Dipper, James, and Mathas, and an algebra constructed to maintain the type B Schur duality of Bao, Wang, and Watanabe, introduced by Lai and Luo. By writing the latter algebra as an idempotent truncation of the former, we leverage its properties to establish cellularity and study the crystal graph structure of the simples of the endomorphism algebra, investigating parameter values at which these algebras are Morita equivalent and quasi-hereditary. We then investigate its blocks, also by comparison with those of the cyclotomic $q$-Schur algebra and type B Hecke algebra.
Keirn Munro
Wednesday, June 26, 2024
10:00 a.m. (sharp)
BA6183/ Zoom Web Conference
PhD Candidate: Keirn Munro
Supervisor: Marco Gualtieri
Thesis title: ![]() Simplicial Approximation of the Hodge Laplacian Using Cauchy Sequences of Hilbert Complexes
Simplicial Approximation of the Hodge Laplacian Using Cauchy Sequences of Hilbert Complexes
Discrete differential geometry arises from the use of discrete spaces such as graphs, simplicial, cubical, or polyhedral complexes for modeling geometric structures on manifolds. A common practice in this work is to transport structures on smooth manifolds to discrete counterparts in a process referred to as discretization. Discretizations often appear as elements of a sequence that approximates the smooth structure on the manifold through some measure of convergence. Algorithms which produce such sequences are highly sought after for computational applications but frequently ignore deeper structural relationships between successive discrete models.
This thesis makes contributions to the discretization of Hodge theory through the construction of a framework that serves to axiomatize a foundational set of results in the field. The salient feature of this framework is the ability to directly measure the difference in approximation accuracy between discretizations without reference to the overarching smooth structure. This provides a Cauchy-type characterization of sequences of discretizations while opening the scope of inquiry to a much larger class of problems involving the analysis of Hodge Theory through Cauchy sequences.
Belal Abuelnasr
Wednesday, June 26, 2024
2:00 p.m. (sharp)
BA6183/ Zoom Web Conference
PhD Candidate: Belal Abuelnasr
Supervisor: Adam Stinchcombe
Thesis title: Modelling and Simulating Retinal Dynamics and Physiology
We present a detailed physiological model of the (human) retina that includes the biochemistry and electrophysiology of phototransduction, neuronal electrical coupling, and the spherical geometry of the eye. The model is a parabolic-elliptic system of partial differential equations based on the mathematical framework of the bi-domain equations, which we have generalized to account for multiple cell-types. We discretize in space with non-uniform finite differences and step through time with a custom adaptive time-stepper that employs a backward differentiation formula and an inexact Newton method. A refinement study confirms the accuracy and efficiency of our numerical method. We generalize our time-stepping scheme to higher order and derive estimates for the corresponding local truncation errors. Numerical simulations using the model compare favourably with experimental findings, such as desensitization to light stimuli and calcium buffering in photoreceptors. Other numerical simulations suggest an interplay between photoreceptor gap junctions and inner segment, but not outer segment, calcium concentration. Applications of this model and simulation include analysis of retinal calcium imaging experiments, the design of electroretinograms, the design of visual prosthetics, and studies of ephaptic coupling within the retina.
Julian Ransford
Thursday, June 27, 2024
11:00 a.m. (sharp)
BA6183/ Zoom Web Conference
PhD Candidate: Julian Ransford
Supervisor: Balint Virag
Thesis title: Directed polymers in the intermediate disorder regime and the Seppäläinen–Johansson model
See poster for abstract.
Daniel Calderon Wilches
Wednesday, July 3, 2024
2:00 p.m. (sharp)
BA6183/ Zoom Web Conference
PhD Candidate: Daniel Calderon Wilches
Supervisor: Stevo Todorcevic & Ilijas Farah
Thesis title: Forcing in Analysis and Combinatorics
In this thesis, we explore some new applications of the forcing technique in the context of Analysis and Combinatorics by:
- Constructing a model of Set Theory in which strong measure zero subsets of the real line are meager-additive while Borel’s conjecture fails, answering a long-standing question due to Bartoszy´nski and Judah.
- Constructing a model of Set Theory in which Jensen’s ♢ℵ1 fails, there is a counterexample to Naimark’s Problem, and there is a separably represented C∗-algebra with exactly two inequivalent irreducible representations. Such a C∗-algebra cannot satisfy the conclusion of Glimm’s Dichotomy Theorem.
- Studying families of infinite block sequences of elements of the space FINk, Ramsey properties of such families, and Ramsey properties localized on selective or semiselective coideals and ultrafilters.
Amirmasoud Geevechi
Tuesday, July 9, 2024
11:00 a.m. (sharp)
BA6183/ Zoom Web Conference
PhD Candidate: Amirmasoud Geevechi
Supervisor: Robert Jerrard
Thesis title: A Gluing Problem for a Gauged Hyperbolic PDE
In this thesis, we study the dynamic Abelian Higgs model in dimension 3 at the critical coupling. This is a system of partial differential equations which enjoys local symmetries known as gauge transformations. The stationary finite energy solutions to these equations in dimension 2 have been classified by Jaffe and Taubes in 1980, the so called vortex configurations. In 1992, Stuart has proved that one can construct solutions near the critical coupling regime in dimension 1+2 whose dynamics are approximated by a finite dimension Hamiltonian system on the moduli space which reduces to the geodesic flow at the critical coupling.
In this project, we study how one can glue the vortex configurations to find dynamic solutions in dimension 3. More precisely, we prove that one can construct solutions which are approximated by wave maps to the moduli space of vortex configurations. The proof involves an ansatz to construct approximate solutions and then add perturbations. In the ansatz, we go through an iterative mechanism to reduce the error of the approximate solution so that it is prepared to be perturbed to find an honest solution.
In both steps of the project, the ansatz and perturbation, the choice of gauge is crucial. It is noteworthy that the choices of gauge are different in these two steps. We proceed by a choice for gauge, simplify the equations and then we have to decompose the quantities into two components, the zero modes (the tangent vectors to the moduli space) and the orthogonal complement to zero modes. According to the Higgs mechanism, stability is available for the components orthogonal to zero modes. In this regard, in the ansatz, the dynamics of zero modes is designed in such a way that the orthogonality condition to zero modes is satisfied. In the perturbation part, the dynamics of zero modes is forced by the evolution of orthogonal components. Obtaining desired estimates for the tangential
part requires taking advantage of explicit structure of equations, rather than the usual estimates. Also, the number of iterations in the ansatz should be high enough so that the desired estimates hold for the tangential part.
Ilia Kirillov
Monday, June 24, 2024
11:00 a.m. (sharp)
BA6183/ Zoom Web Conference
PhD Candidate:Ilia Kirillov
Supervisor: Boris Khesin
Thesis title: Coadjoint orbits of symplectomorphism groups of surfaces
In this thesis, we classify generic coadjoint orbits for the action of symplectic (equivalently, areapreserving) diffeomorphisms of compact symplectic surfaces with or without boundary. This completes V. Arnold’s program of studying Casimir invariants of incompressible fluids in 2D. To obtain this classification, we first solve an auxiliary problem, which is of interest by itself: classify generic Morse functions on surfaces with respect to the action of area-preserving diffeomorphisms. As a technical tool, we prove an analog of Morse-Darboux lemma in the case of a singular point on the boundary. We also generalize all the results above to the case of non-orientable surfaces without boundary.
David Pechersky
Wednesday, June 19, 2024
11:00 a.m. (sharp)
BA6183/ Zoom Web Conference
PhD Candidate: David Pechersky
Supervisor: Ilia Binder
Thesis title: Discrete Complex Analysis and Convergence of Observables on Orthodiagonal Maps
Discrete complex analysis is the study of discrete holomorphic functions. These are functions defined on graphs embedded in the plane that satisfy some discrete analogue of the Cauchy-Riemann equations. While the subject is classical, it has seen a resurgence in the past 20-30 years with the work of Kenyon, Mercat, Smirnov, and many others demonstrating the power of discrete complex analysis as a tool for understanding 2D statistical physics at criticality.
In this talk, we’ll discuss how discrete complex analysis can be applied to solve a purely deterministic problem for a very general class of discretizations of 2D space accommodating a notion of discrete
complex analysis.
Jim Shaw
Thursday, June 13, 2024
11:00 a.m. (sharp)
BA6183/ Zoom Web Conference
PhD Candidate: Jim Shaw
Supervisor: Yun William Yu
Thesis title: ![]() Practical and theoretical problems in biological sequence comparison.pdf
Practical and theoretical problems in biological sequence comparison.pdf
DNA sequencing technologies have revolutionized the study of biology, allowing unprecedented access to the blueprint of life – our genomes. As these technologies have matured, massive amounts of DNA sequences are now becoming available for computers to analyze. The increasing throughput of these technologies has rendered old algorithms unusable. In this thesis, we first build a principled mathematical foundation for approximate DNA string matching, also called sequence alignment. We then show that using theoretically-backed approaches can result in faster and better software implementations, resulting in useful new tools for biologists.
In Chapter 3, we rigorously analyze how to subsample DNA strings to speed up alignment while retaining sensitivity. We show how to determine a sampling algorithm’s conservation, which is a measure of how sensitively it can match strings. Surprisingly, different sampling methods have vastly different conservation even when retaining the same amount of “information”. We show that modifying existing software to use better subsampling algorithms gives more sensitive results.
In Chapter 4, we provide the first non-trivial runtime and accuracy bounds on a widely-used DNA alignment algorithm called seed-chain-extend. We break the worst-case quadratic runtime barrier of sequence alignment by performing an average-case analysis under a probabilistic evolutionary model of DNA sequence. Our results are concordant with algorithmic results on real data and provide new insights into the rigorous analysis of sequence alignment.
In Chapter 5, we utilize the subsampling and the seed-chain-extend approaches analyzed in Chapters 3 and 4 to build a new genome-genome comparison method and software called skani. skani can estimate the evolutionary divergence between two genomes > 25 times faster than previous algorithms. We show that skani can compare hundreds of thousands of genomes in seconds on a standard desktop computer, enabling large-scale comparisons not possible before.
Adrian She
Wednesday, June 12, 2024
11:00 a.m. (sharp)
BA6183/ Zoom Web Conference
PhD Candidate : Adrian She
Supervisors: Toniann Pitassi, Henry Yuen
Thesis title: Algebraic Methods in Query and Proof Complexity
Algebraic methods have become a powerful tool for analyzing the complexity of various computational models, including low-depth circuits, algebraic proofs, and quantum query algorithms. In particular, the complexity of computing a function in these models is related to whether or not the function admits a lowdegree polynomial approximation. In this thesis, we present two novel applications of algebraic methods in computational complexity theory.
In the first part of the thesis, we study unitary property testing, where a quantum algorithm is given query access to a black-box unitary and has to decide whether or not it satisfies some property. In addition to containing the classical query complexity model as a special case, this model also contains “inherently quantum” problems that have no classical analogue. Our main contribution is a generalized polynomial method for analyzing the complexity of unitary property testing problems. By leveraging connections with
invariant theory, we apply this method to obtain lower bounds on problems such as determining recurrence times of unitaries, approximating the dimension of a subspace, and approximating the entanglement entropy of a state. We also present a candidate problem towards an oracle separation of QMA and QMA(2), a long standing open question in quantum complexity theory.
In the second part of the thesis, we study the tensor isomorphism problem (TI), which has recently emerged as having connections to multiple areas of research, including quantum information theory, postquantum cryptography, and computational algebra. However, the current best upper bound is essentially the brute force algorithm. Being an algebraic problem, the study of tensor isomorphism naturally lends itself to algebraic and semi-algebraic proof systems such as the polynomial calculus (PC) and sum-of squares
(SoS). We show a Ω(n) lower bound on PC degree or SoS degree for tensor isomorphism and a non-trivial upper bound for testing isomorphism of tensors of bounded rank. Along the way, we also show that PC cannot perform basic linear algebra in sublinear degree, such as comparing the rank of two matrices. We introduce a strictly stronger proof system, called PC + Inv, which enables linear algebra to be done in low degree. We conjecture that even PC + Inv cannot solve TI in polynomial time either, and highlight many other open questions about proof complexity approaches to TI.
Joaquin Sanchez Garcia
Wednesday, June 12, 2024
2:00 p.m. (sharp)
BA6183/ Zoom Web Conference
PhD Candidate: Joaquin Sanchez Garcia
Supervisor: Robert McCann
Thesis title: 4 Problems in optimal transportation
This thesis is devoted to the study of 4 different problems for which we use the theory of optimal transportation:
1. The generalization of the Schrödinger Problem to synthetic Lorentzian geometries. 2. The small time existence for solutions for the aggregation equation on compact Riemannian manifolds for non-regular interaction potentials via the minimizing movement scheme. 3. The technique of measure pre-conditioning general Machine-Learning tasks and Domain Adaptation transfer learning. 4.The generalization of an economic model of Roy for partition of labor including occupational choice as a constraint.
1 Part 1: The Schrödinger problem in synthetic Lorentzian geometries
The Schrödinger problem refers to the minimization of relative entropy with respect to a reference measure. The Schrödinger problem is usually analyzed in two related formulations: the static and the dynamic Schrödinger problems. We study both approaches. One of the main questions of the Schrödinger problem is whether or not the solutions to the entropically regularized optimal transport problem converge to solutions of the optimal transport problem. In the dynamical setting, this property amounts to study the Large Deviation Principles of the reference measure. We study a Levy-like construction which emulates the behaviour of Brownian bridges which allows us to recover a partial version of the entropic convergence in the non-smooth Lorentzian case.
2 Part 2: The aggregation equation via the minimizing movement scheme in compact Riemannian manifolds
We study the small-time existence of solutions for non-smooth potentials via the minimizing movement scheme. The theory of gradient flows in metric spaces does not consider a potential non-regularity of potentials in the cut-locus. The presence of the cut-locus presents a difficulty for the JKO scheme to choose a direction, nevertheless we show explicitly a time bound for which we can flow the minimizing movement scheme.
3 Part 3: Measure Pre-conditioning in Machine-Learning
We study a new technique to improve convergence of algorithms for specific ML-tasks. We show that if the modifications of the problem at level n (sample size) are done in a specific way (full learner recovery
systems) we can show analytical subsequential convergence to the original model. This technique seems to be specifically important for Domain Adaptation in transfer learning.
4 Part 4: Generalizing an economic model of Roy for labor partition using occupational choice as a constraint
We study the analytical properties of a generalization of the economic model for labor force partition studied by Dr. Roy. The new model proposed by Dr. Siow, includes occupational choice as a constraint rather than a consequence. This difference allows us to rewrite the problem in an analytically useful way.
Saeyon Mylvaganam
Monday, June 10, 2024
2:00 p.m. (sharp)
BA6183/ Zoom Web Conference
PhD Candidate : Saeyon Mylvaganam
Supervisors: Stefanos Aretakis
Thesis title: The Null Gluing Problem and Conservation Laws for Maxwell's Equations
We study the null gluing problem for Maxwell’s equations along null hypersurfaces. By studying a weaker formulation of the gluing problem, which we call the kth-order gluing problem, we classify all possible conservation laws by proving that they are the only obstructions to gluing. We derive sets of conserved charges for the zeroth-order gluing problem along general null hypersurfaces and the first-order gluing problem along extremal horizons. We derive an elliptic structure related to a foliation with 2-spheres of a null hypersurface, using a similar method introduced in [9] by Aretakis. We also show the non-existence of zeroth-order conservation laws along extremal horizons and the non-existence of kth-order conservation laws for spherically symmetric extremal horizons by using a hierarchy of v-weighted integrals of the Maxwell equations. Finally, we determine how the space of these conserved charges changes under a change of foliation by understanding the gauge covariance of the elliptic structure.
Tomas Dominguez Chiozza
Monday, February 12th, 2024
10:00 a.m. (sharp)
BA6183/ Zoom Web Conference
PhD Candidate: Tomas Dominguez Chiozza
Supervisor: Dmitry Panchenko
Thesis title: ![]() A Hamilton-Jacobi approach to the stochastic block model
A Hamilton-Jacobi approach to the stochastic block model
This thesis addresses the problem of recovering the community structure in the stochastic block model with two communities. The stochastic block model is a random graph model with planted clusters widely employed as the canonical model to study clustering and community detection. The focus is on the fundamental limits of community detection, quantified by the asymptotic mutual information between the observed network and the actual community structure. This mutual information is studied using the Hamilton-Jacobi approach, pioneered by Jean-Christophe Mourrat.
The first contribution of this thesis is a detailed description of the Hamilton-Jacobi approach, and its application to computing the limit of the mutual information in the dense stochastic block model, where the average degree of a node diverges with the total number of nodes. The main novelty is a wellposedness theory for Hamilton-Jacobi equations on positive half-space that leverages the monotonicity of the non-linearity to circumvent the imposition of an artificial boundary condition as previously done in the literature.
The second contribution of this thesis is a novel well-posedness theory for an infinite-dimensional Hamilton-Jacobi equation posed on the set of non-negative measures and with a monotonic non-linearity.
Such an infinite-dimensional Hamilton-Jacobi equation appears naturally when applying the Hamilton- Jacobi approach to the sparse stochastic block model, where the total number of nodes diverges while the average degree of a node remains bounded. The solution to the infinite-dimensional Hamilton-Jacobi equation is defined as the limit of the solutions to an approximating family of finite-dimensional Hamilton- Jacobi equations on positive half-space. In the special setting of a convex non-linearity, a Hopf-Lax variational representation of the solution is also established.
The third contribution of this thesis is a conjecture for the limit of the mutual information in the sparse stochastic block model, and a proof that this conjectured limit provides a lower bound for the asymptotic mutual information. In the case when links across communities are more likely than links within communities, the asymptotic mutual information is known to be given by a variational formula. It is also shown that the conjectured limit coincides with this formula in this case.
Kevin (Min Seong) Park
Wednesday, December 13, 2023
3:00 p.m.
BA6183/ Zoom Web Conference
PhD Candidate: Kevin Min Seong Park
Supervisor: Adam Stinchcombe
Thesis title: ![]() Temporal Difference Learning for viscous incompressible flow
Temporal Difference Learning for viscous incompressible flow
This thesis presents a stochastic numerical method for computing viscous incompressible flow. By Itô’s lemma, the solution to a linear parabolic PDE is a martingale over an appropriate probability measure induced by Brownian motion. Given an initial boundary value problem, a functional corresponding to the martingale condition is minimized numerically through deep reinforcement learning. This methodology is well-suited for high dimensional PDEs over irregular domains, as it is mesh-free and sampling techniques can avoid the curse of dimensionality.
The extension to computing viscous incompressible flow is done by first formulating a martingale condition for the viscous Burgers’ equation. Its solution is obtained by a fixed point iteration for which a proof of convergence in L2 is provided. The constrained minimization problem subject to divergence-free vector fields is designed for the incompressible Navier-Stokes equations. The velocity is determined without the pressure gradient. The stochastic numerical method avoids difficulties arising from coupling of velocity and pressure terms by globally maintaining incompressibility. Furthermore, pressure can be recovered from the computed velocity in a post-processing step.
The numerical implementation details are provided, including errors from statistical sampling. Simulations of various flow scenarios are showcased, including those with analytical solutions such as Stokes’ flow in a revolving ball, Poiseuille flow, and the Taylor-Green vortex. Additional validation is acquired from comparing against numerical solutions for cavity flow, and flow past a disk. Analysis is undertaken to determine bounds on the statistical and numerical error. A number of improvements in deep learning and generalizations to broader classes of PDES are proposed as possible avenues of future research. Software is available at github.com/mskpark/DRLPDE
Tomas Kojar
Thursday, May 23, 2024
11:00 a.m. (sharp)
BA6183/ Zoom Web Conference
PhD Candidate: Tomas Kojar
Supervisor: Ilia Binder
Thesis title: ![]() Inverse of the Gaussian multiplicative chaos.pdf
Inverse of the Gaussian multiplicative chaos.pdf
In this thesis we do a fundamental study of the Gaussian multiplicative chaos (GMC) on the real line enroute to an interesting problem in the field of Schramm Loewner evolution (SLE) curve. This is a singular measure that is the limit of the integral of an exponentiated Gaussian field with logarithmic covariance. It is strictly monotonic and so it has an inverse that we study its single-point and multi-point moments and correlation structure.
The interesting problem is a coupling between the Gaussian free field and the SLE curve. In the 2010 - work "Conformal weldings of random surfaces: SLE and the quantum gravity zipper" S.Sheffield initiated an approach of coupling those two random objects by constructing the quantum zipper joint process. Here we follow an alternative perspective initiated around the same time in the 2009-work "Random Conformal Weldings" K. Astala, P. Jones, A. Kupiainen, E. Saksman using the Beltrami equation and the Lehto
estimates. In particular, they proved a conformal welding result for the GMC measure on the unit circle. In the thesis, we prove the analogous result for the inverse of the GMC measure on the unit circle.